Queue ADT, implementation and interface

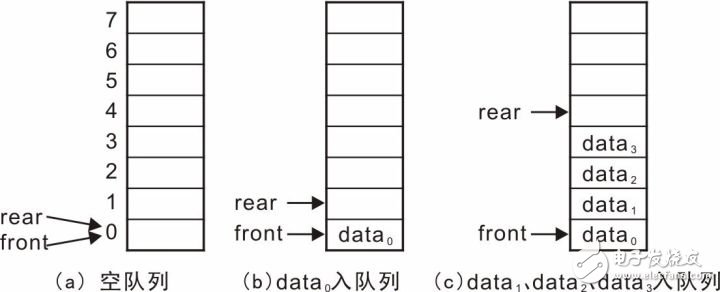
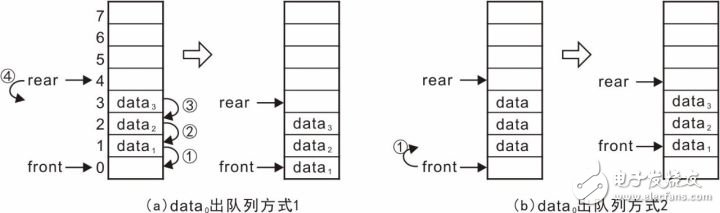
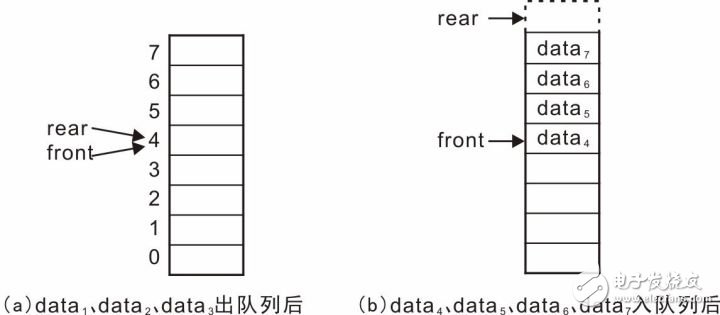
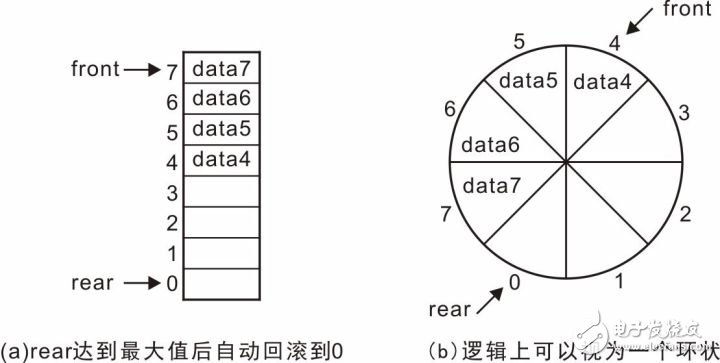
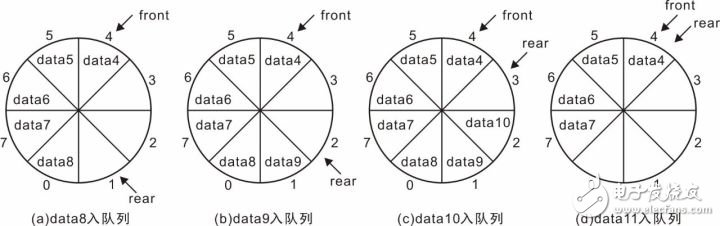
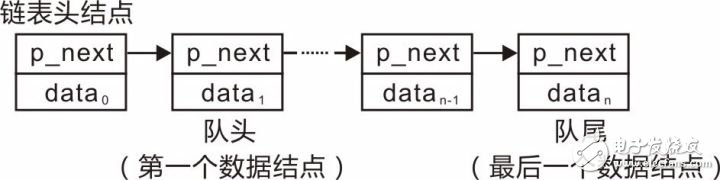
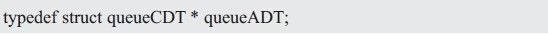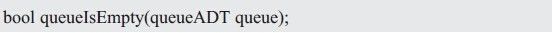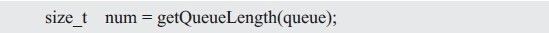Professor Zhou Ligong's years of hard work "Programming and Data Structure" and "Programming for AMetal Framework and Interface (I)", the electronic version has been distributed to electronic engineers and college groups for free, replying to the public number [programming] Read it online. After the publication of the book content, there was a learning boom in the electronics industry. Authorized by Professor Zhou Ligong, this public number has serialized the contents of the book "Programming and Data Structure" and is willing to share it.

The third chapter is the algorithm and data structure. This article is 3.6 queue ADT.

> > >    3.6.1 Establishing an abstraction

The queue can be simply described as: the queue is a special container that limits the insertion position at the end of the container (the tail of the queue), and the delete position at the head of the container (the head of the queue) is a "first in, first out" (First Linear structure of In-First Out, FIFO). For example, if you queue up to buy tickets, people join the queue from the end of the team and leave the team after buying the tickets (assuming no one is plugged in). The schematic is shown in Figure 3.28.

Figure 3.28 Schematic diagram of the queue

Its abstract definition is as follows:

Type name: Queue

Type attribute: store a series of items

Type operation: Add items from the end of the team, delete items from the team head, determine whether the queue is empty, determine whether the queue is full, and determine the number of items in the queue.

> > > 3.6.2 Establishing an interface

The interface is provided to the user via a header file. First create a header file named queue.h. In the interface file, you need to include two parts: one, the definition of the abstract type queueADT; and the second, the operation function of each queue ADT.

1, define the abstract type queueADT

Similar to the stack, use the struct type to represent a queue. In the header file, you only need to define one struct type. The details of the actual definition of the structure, the specific members contained need not be defined in the header file, and the definition is completed by the concrete implementation. Define the abstract type queueADT as follows:

2, interface function declaration

Create queue

Before using the queue, you must create a queue correctly, so you need to provide a function to create a new queueADT. Its function prototype is as follows:

Postcondition: Return to the queue.

The form of its call is as follows:

Destroy queue

When a queue is created, the specific implementation allocates the storage space related to the queue according to the actual situation, such as the storage space of the queue object itself and the storage space of the queue item. Therefore, when a queue is not in use, the queue-related memory space should be released to destroy a queue. The destroyed queue no longer exists and cannot be used. Its function prototype is as follows:

Precondition: queue is the previously created queue;

Postcondition: Releases all memory associated with the queue, the queue is destroyed and is no longer valid.

The form of its call is as follows:

Add items from the end of the queue (into the queue)

The user can add new elements from the tail of the queue to the queue through this function. The function prototype is as follows:

Pre-condition: queue is the previously created queue, and value is the data to be added to the end of the queue;

Postcondition: If the queue is not full, add value to the end of the team, the function returns true; otherwise, the queue is full, the queue remains unchanged, the function returns false.

The form of its call is as follows:

Remove items from the head of the team (out of the queue)

The user can remove an element from the head of the queue through this function. The function prototype is as follows:

Precondition: queue is the previously created queue, p_value is a pointer to the variable storing the value of "moving out of the queue";

Postcondition: If the queue is not empty, copy the value of the team header to *p_value and delete the current head, the function returns true; otherwise, the queue is empty, the function returns false.

The form of its call is as follows:

Determine if the queue is empty

The function prototype for judging whether the queue is empty is as follows:

Precondition: queue is the previously created queue;

Postcondition: Returns true if the queue is empty, otherwise returns false.

The form of its call is as follows:

Determine if the queue is full

The function prototype that determines whether the queue is full is as follows:

Precondition: queue is the previously created queue;

Postcondition: Returns true if the queue is empty, otherwise returns false.

The form of its call is as follows:

Determine the number of elements in the queue

The function prototype for determining the number of elements in the stack is as follows:

Precondition: queue is the previously created queue;

Postcondition: Returns the number of elements in the queue.

The form of its call is as follows:

Listing 3.70 Abstract Queue Interface (queue.h)

> > > 3.6.3 Implementation and use interface

Before implementing the queue, you first need to determine which data storage structure to use. In general, you can store data in a contiguous memory space, such as using arrays or dynamically allocating a block of memory; you can also store data using a non-contiguous list structure.

1, sequential queue

Before implementing the queue, let's analyze the principle of the sequential queue. The sequential queue uses a contiguous memory space. It is assumed that the front and rear variables are used to indicate the position of the head and tail respectively. Initially, the queue is empty, and both the head and the tail are 0. See Figure 3.29 (a ).

When adding data from the end of the team, rear increases backwards. If data0 enters the queue, the schematic diagram is shown in Figure 3.29 (b). At this time, the front of the team remains unchanged, and the rear of the team increases by 1, and continues to queue. The schematic diagram of data1, data2, and data3 after entering the queue is shown in Figure 3.29 (c).

Figure 3.29 Schematic diagram of the queue - into the queue

When removing data from the head of the team, for example, after removing data0, the data pointed to by the front of the team must be updated to data1. There are two ways: First, the front remains motionless, moving all the data forward one space. As shown in Figure 3.30(a); the second is that the data remains unchanged, and the front is incremented by 1, making it point to data1. Obviously, moving all the data forward one space has a large number of data copies. The more data in the queue, the more data copy operations, the lower the efficiency, and adding the value of front to 1 is very simple and fast, therefore, In general, the second treatment is chosen.

Figure 3.30 Schematic diagram of the queue - outbound

According to mode 2, data1, data2, and data3 are continuously queued. The schematic diagram is shown in Figure 3.31(a). At this time, there is no valid data in the queue. The rear is equal to the front, and the queue is empty.

If the data inbound operation continues, the data4, data5, data6, and data7 are sequentially entered into the queue. See Figure 3.31(b). Since the queue element has been stored in the storage address of the highest address, the real has pointed to the invalid address. In this state, you can no longer simply add data to the end of the team in the same way as before, otherwise the program will be abnormal because the array is out of bounds.

Figure 3.31 Continue to queue and queue operations

So, in the case shown in Figure 3.31(b), can you add new elements? Obviously, there is still half of the space at this time without filling the data. A clever way to use the free space is to automatically roll back to 0 when the value of the rear or front exceeds the maximum value. In Figure 3.31(b), the real has exceeded the maximum address, so roll it back to 0, as shown in Figure 3.32(a). That is, logically, the sequential queue is treated as a ring space, as shown in Figure 3.32(b). After entering the queue, it is no longer simple to add 1 to the rear value. Instead, when adding 1, it determines whether the maximum address space has been exceeded. If it is exceeded, the value of rear is set to 0 again.

Figure 3.32 Circular Queue

After considering the storage space as a ring, it will be easier to understand the inbound and outbound operations. When entering the queue, only the space pointed to by the data storage value should be stored. After the storage is completed, the value of the rear is updated to point to the next storage unit. When out of the queue, the data in the space pointed to by the front is taken out, and the value of the front is updated to point to the next storage unit.

In particular, when front and rear are equal, it means that the queue is empty and cannot be queued. Correspondingly, when is the queue full? On the basis of Figure 3.32(b), continue to add data8, data9, data10, and data11 to the queue, so that all idle cells store data. You can see that the schematic diagram after adding each data is shown in Figure 3.33.

Figure 3.33 data8~data11 are queued in sequence

When data11 is added to the queue, all storage units store data. At this point, the queue is full. You can see that the current front is equal to rear, and the front and rear are equal when the queue is empty. It can be seen that it is impossible to judge whether the queue is "full" or "empty" only because the front and the rear are equal. How to solve it? The easiest way is to add a flag. When the data is queued and the front and the rear are equal, set the flag bit 1 to mark the current "full" state. There is also a clever way to actually use one storage unit. When the front is in the next position of the rear, that is, the state shown in Figure 3.33(c), the queue is considered full and no new elements are allowed to join the queue. The advantage of this method is that there is no need to add extra flags, just modify the way to determine whether the queue is full, but its shortcomings are also obvious, it will waste a data storage space. In fact, when adding a flag, the added flag also needs to occupy memory space.

At this point, it analyzes the implementation method of whether the queue is queued, outbound, and whether the queue is empty, and whether the queue is full. The last operation is not mentioned, that is, the number of elements in the queue is determined.

In essence, it is very simple to find the number of elements. You only need to subtract the tail value of the team tail from the front of the team. The difference is the number of data between the head and the tail. However, special circumstances need to be considered, because in the loop queue, the value of the tail of the team may be smaller than the value of the head of the team, as shown in Figure 3.34 (a), (b), (c). At this point, their difference is a negative value, as shown in Figure 3.35(a): rear = 1, front = 4, their difference is -3, and the actual number of elements is 5. It can be seen that when the value is negative, you only need to add the size of the storage space (8 in the example).

The above analysis of the principle of the circular queue, then use the program to implement the various interfaces of the queue, the implementation code is stored in the queue.c file. When establishing an interface, the type of the abstract queue is first defined in the header file:

The structure type struct queueCDT here is only declared, and there is no specific definition. Therefore, regardless of the implementation, you need to implement the definition of the struct queueCDT type.

Assuming that the contiguous space used is dynamically allocated by malloc, it is necessary to include a pointer to the contiguous space's first address in the struct to use this memory space. In addition, in the analysis of the above principle, you need to use front and rear to indicate the position of the head and tail respectively, so you need to include these two members in the queue structure, and define the queue structure type as:

After understanding the principles of the various operations of the queue, it is easier to implement. See Listing 2.34 for details.

Listing 3.71 Implementation of a sequential queue (queue.c)

In the implementation of the getQueueLength() function, it is clever to avoid using the if statement to determine whether the difference between the rear and the front is negative. If the difference is positive or negative, the MAXQSIZE (the size of the queue) is added. At this point, if the difference is negative, you can get the correct result, but if the difference is positive, the result will be exactly MAXQSIZE, so you need to take the result to MAXQSIZE to discard the MAXQSIZE that may be extra. To ensure the correctness of the results.

2, chain queue

In the chain queue, the storage space of each data may be discontinuous, and the list based on the linked list (assuming the data field is int type) is shown in Figure 3.36.

Figure 3.36 Schematic diagram of the chain queue

It should be noted that the link header node represents the link header, which is defined for the convenience of adding node operations and does not carry valid application data. The subsequent node is the active node, so the team leader is the first valid data node, and the team tail is the last valid data node.

The queue is to add a new element to the end of the list, and the queue is to remove the first data node. These operations already have corresponding interfaces in the linked list program. Therefore, based on the previous linked list program, implementing chain queuing is very easy. In the queue structure, only the list header node needs to be included, and no members such as front and rear are needed. Define the queue structure body type as:

If the data type of each node in the queue is of type int, the corresponding linked list node type is:

An example of the implementation of a chain queue is shown in Listing 3.72.

Listing 3.72 Implementation of the chain queue (queue_list.c)

For most operations, the linked list already provides the appropriate interface, so it is very easy to queue, queue, and judge whether it is full or empty. A little more complicated is to get the number of elements in the queue, which needs to traverse the entire linked list. Whenever it is traversed to a node, the value of the counter count is incremented by one (the address of count is passed through the p_arg parameter of the traversal function), and the traversal ends. After that, the value of the counter is the number of elements in the queue.

In the implementation of the queue function, each time you need to add a new node to the end of the list, and for a singly linked list, the efficiency of adding the node directly to the end of the list is very low, and you need to traverse from the beginning every time. The actual addition can only be performed until the last node is found. How to solve this problem? The easiest way is to use a doubly linked list, but the doubly linked list needs to occupy more memory. At the same time, in the implementation of the queue, there is no need for a doubly linked list. It is not necessary to randomly search for the last node. Obviously, the doubly linked list is used here. A little "big problem". To grasp a core problem, you need to add a new node to the end of the list. If you use a pointer p_rear to point to the tail node, you can add the node directly to the node pointed to by p_rear when adding the node to the end of the list. After the point, there is no need to traverse the linked list from the beginning, that is, "slist_add (p_head, p_rear, p_node);".

After the end of the addition, the new p_node node is the new tail node, so you need to update the value of p_rear to point to the new tail node, which is "p_rear = p_node;". P_rear can be used as a member of the queue structure for use. In this way, the reader can try to modify the queue function and improve the efficiency of the queue.

For the user, there is no need to care about the specific implementation of the queue. As long as you correctly grasp the use of the interface (preconditions and postconditions), you can write applications that use queues. The sample program for invoking integers and then out of the queue is detailed in Listing 2.35.

Listing 3.73 Sample program using the queue interface